Philadelphia Minimum Span Instances

Introduction

The Philadelphia instances were among the first discussed in the literature [Anderson, 1973]. The sites in Philadelphia were modeled on a hexagonal grid (see Figure 1). Each site demands a high number of frequencies, the multiplicity of the sites. Adjacent sites should not be admitted to use the same frequencies, and antennae at the same site should not use adjacent frequencies either. Variants of this structure use different re-use distances, for instance (d0,d1,d2)=(3,2,1) meaning that antennae in cells of distance 3 can use the same frequency and so on (the distance between 2 adjacent cells is taken as unit distance).

Characteristics

network structure instance P1
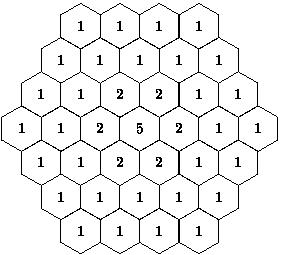
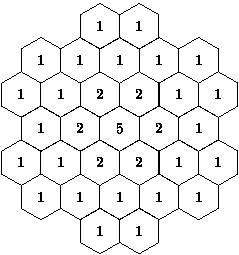
Figure 1: Network structure Philadelpia instances Figure 2: Demand of instance P1

The original instance and certain variants are widely used afterwards to substantiate algorithms and lower bounds for the MS-FAP. The Philadelphia instances are characterized by 21 hexagons denoting the cells of a cellular phone network around Philadelphia (see Figure 1). Until recently, it was common practice to model wireless phone networks as hexagonal cell systems. For each cell, a demand cv is given. Figure 2 shows the demand for the original instance P1, whereas the table below contains the demand vectors of all instances. In conformity with [Valenzuela et al., 1998], the instances are denoted by P1-P9. Some of them are also appointed in [Hurley et al., 1997] as E3-E9. In [Avenali et al., 2002] more variants are considered. These are numbered P1-P19. Since these names do not correspond with the ones in [Valenzuela et al., 1998] we rename them as p1-p19 (not all are included in this overview).
reuse distances P1, P3, P5, P7, P9 reuse distances P2, P4, P6
Figure 3: Resuse distances P1, P3, P5, P7, P9 Figure 4: Resuse distances P2, P4, P6
In the basic model, interference of cells is characterized by a co-channel reuse distance d. No interference occurs if and only if the centers of two cells have mutual distance $\geq d$. In case the mutual distance is less than d (normalized by the radius of the cells), it is not allowed to assign the same frequency to both cells. This pure co-channel case is generalized by replacing the reuse distance d by a series of non-increasing values $d^0,\ldots,d^k$. For instance, P1 the values $d^0,\ldots,d^5$ are $2\sqrt{3},\sqrt{3},1,1,1,0$. So, frequencies assigned to the same site should be separated by at least 4 other frequencies, whereas frequencies assigned to adjacent sites should be at a distance of at least 2, and frequencies assigned to a second and third `ring' of cells should still differ (see Figures 3 and 4). For the other instances, the reuse distances are given in Table 1. The frequency domains of all positive integral values, which implies that minimization of the span is equivalent to minimization of the maximum used frequency. Note that, there is a difference of one between minimum span and maximum used frequency.
Table 1: Demand vectors and reuse distances Philadelphia benchmark instances
instance demand vector cv reuse distances
P1 (E3,p3) (8,25,8,8,8,15,18,52,77,28,13,15,31,15,36,57,28,8,10,13,8) $(2\sqrt{3},\sqrt{3},1,1,1,0)$
P2 (E4,p8) (8,25,8,8,8,15,18,52,77,28,13,15,31,15,36,57,28,8,10,13,8) $(\sqrt{7},\sqrt{3},1,1,1,0)$
P3 (E5,p2) (5,5,5,8,12,25,30,25,30,40,40,45,20,30,25,15,15,30,20,20,25) $(2\sqrt{3},\sqrt{3},1,1,1,0)$
P4 (E6,p7) (5,5,5,8,12,25,30,25,30,40,40,45,20,30,25,15,15,30,20,20,25) $(\sqrt{7},\sqrt{3},1,1,1,0)$
P5 (E7,p1) (20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20) $(2\sqrt{3},\sqrt{3},1,1,1,0)$
P6 (p6) (20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20,20) $(\sqrt{7},\sqrt{3},1,1,1,0)$
P7 (E8,p4) (16,50,16,16,16,30,36,104,154,56,26,30,62,30,72,114,56,16,20,26,16) $(2\sqrt{3},\sqrt{3},1,1,1,0)$
P8 (p9) (8,25,8,8,8,15,18,52,77,28,13,15,31,15,36,57,28,8,10,13,8) $(2\sqrt{3},2,1,1,1,0)$
P9 (E9,p5) (32,100,32,32,32,60,72,208,308,112,52,60,124,60,144,228,112,32,40,52,32) $(2\sqrt{3},\sqrt{3},1,1,1,0)$

Results

Table 2 shows the results obtained on the Philadelphia instances.

Table 2: Results Philadelphia benchmark instances
instance lower bounds optimal value (range) upper bounds
[Gamst, 1986] [Janssen and Kilakos, 1996a, Janssen and Kilakos, 1996b] [Hurley et al., 1997, Smith et al., 1998] [Sung and Wong, 1997] [Heller, 2000] [Avenali et al., 2002] [Hurley et al., 1997] [Hurley et al., 1997] [Hurley et al., 1997] [Valenzuela et al., 1998] [Hurley et al., 1997, Smith et al., 1998] [Allen et al., 1999] [Smith et al., 2000a, Smith et al., 2000b] [Beckmann and Killat, 1999b, Beckmann and Killat, 1999c] [Matsui and Tokoro, 2001] [Avenali et al., 2002] [Sivarajan et al., 1989] [Sung and Wong, 1997] [Sung and Wong, 1997] [Wang and Rushforth, 1996]
Graph Theory Travelling Salesman Problem Diverse methods Graph Theory Graph Theory Integer Programming Best Sequential Algorithm Tabu Search Simulated Annealing Genetic Algorithm Subgraph Extension Subgraph Extension Subgraph Extension Genetic Algorithm Genetic Algorithm Integer Programming Sequential Coloring Generalized Sequential Packing 1 Generalized Sequential Packing 2 Local Search
P1 413 426 426 426 - 426 426 447 428 428 426 426 - - - 426 426 459 440 450 432
P2 413 426 426 426 - 426 426 475 429 438 426 426 - - 426 426 426 446 436 444 -
P3 245 - 257 252 - 257 257 284 269 260 258 257 - - - 257 275 282 291 273 263
P4 245 252 252 252 - 252 252 268 257 259 253 252 - - 252 252 253 268 273 268 -
P5 239 - 239 177 - 239 239 250 240 239 239 - - - - 239 239 - - - -
P6 139 177 178 177 179 177 179 230 188 200 198 - 179 - - 179 183 - - - -
P7 830 - 855 855 - 855 855 894 858 858 856 855 - - - 855 855 - - - -
P8 449 - 524 427 - 523 524 592 535 546 527 - - 524 - 524 524 - - - -
P9 1,664 - 1,713 1,713 - 1713 1,713 1,800 1,724 1,724 - 1,713 - - - - 1713 - - - -

Last modified: Tue Feb 15 15:28:57 CET 2005 by the fapzib.de