 Click here for the picture in a better format by ENCYCLOP∆DIA BRITANNICA.
Click here for the picture in a better format by ENCYCLOP∆DIA BRITANNICA.
There is not "the" frequency assignment problem. Frequency assignment is necessary in many different types of wireless communication networks. Depending on the particular network, the understanding of frequency assignment varies. In the following, several "flavors" of frequency assignment are discribed.
In the last decade, the rapid development of new wireless services like digital cellular phone networks resulted in a run out of the most important resource, frequencies in the radio spectrum. Like with all scarcely available resources, the cost of frequency-use provides the need for economic use of the available frequencies. Reuse of frequencies within a wireless communication network can offer considerable economies. However, reuse of frequencies may also lead to a loss of quality of communication links. The use of (almost) the same frequency for multiple wireless connections can cause an interference between the signals that is unacceptable. The frequency assignment problem balances the economies of reuse of frequencies and the loss of quality in the network. Quantification of the different aspects results in a mathematical optimization problem that can be solved with Operations Research techniques. Depending on the point of view of the researchers, the goal of the network provider, and application specific conditions many different models and algorithms are proposed.
More than a century ago, in the early 1890s, Marconi started to experiment with wireless communication via radio waves. His research resulted in 1897 in the successful transmission of radio waves to a ship at sea over a distance of 29 kilometers. A couple of years later, it was possible to transmit signals across the Atlantic Ocean, and already in 1905 many ships were using wireless telegraphy to communicate with shore stations. The importance of Marconi's invention can be demonstrated with for example the sinking of the Titanic. Without the equipment to communicate with other ships and shore stations, the disaster would have been considerably larger than it was. In 1909, Marconi received the Nobel Prize in physics for his pioneering work on the wireless telegraph. Continuing improvements of the equipment resulted in the establishment of wireless telephony between Virginia and Paris in 1915. After World War I, radio broadcasting became more and more popular, first on an amateur level, later by professional broadcasters. Experimental television broadcasting already began in the 1930s and was successfully introduced to the mass market beginning in the end of the 1940s. In the last 50 years, the radio spectrum has been explored for wireless communication in many different ways. For example, space missions are not possible without communication via radio waves. It is not only used for voice communication with astronauts, but also for the navigation of the space crafts. Nowadays radio waves are used for wireless telegraphy, radio broadcasting, television, cellular telephone networks, radar, navigational systems (air and sea traffic control), military communication, and space communication.
Each application uses a specific part of the radio spectrum. The frequencies that can be used for wireless communication range from 3 kilohertz to 300 gigahertz. These values correspond to wavelengths between 1 mm and 100 km. The figure below indicates which frequencies are currently used for which application. The most popular applications (radio, television, and cellular phone) use frequencies in the very high frequency (VHF) and ultra high frequency (UHF) spectrum. The use of frequencies for an application is regulated by the International Telecommunication Union (ITU) and national agencies. They issue licenses to use certain frequencies.
 Click here for the picture in a better format by ENCYCLOP∆DIA BRITANNICA.
Click here for the picture in a better format by ENCYCLOP∆DIA BRITANNICA.
Wireless communication between two points is established with the use of a transmitter and a receiver. The transmitter generates electrical oscillations at a radio frequency: the carrier frequency. Oscillations at a radio frequency can be modulated either via the amplitude or the frequency itself. The receiver detects these oscillations and transforms them into sounds or images. When two transmitters use (almost) the same carrier frequency, they may interfere. The level of interference depends on many aspects such as the distance between the transmitters / receivers, the geographical position of the transmitters, the power of the signal, the direction in which the signal is transmitted, and the weather conditions. In case the level of interference is high, the received signal may drop below the signal-to-noise ratio, which causes an unacceptable loss of quality. However, the limited availability of frequencies causes their reuse by multiple transmitters within one and the same network.
As a consequence, an operator should carefully choose the frequencies on which each station transmits to avoid high interference-levels. The selection of the frequencies in such a way that interference is avoided, or second best, is minimized, is called the Frequency Assignment Problem (FAP). Depending on the application, the conditions that should be satisfied by the frequency plan may vary. Therefore, it is not surprising that many different approaches have been suggested in the literature to solve this problem. A survey of the most recent approaches is presented in [Koster, 1999] (see also [Murphy et al., 1999, Aardal et al., 2000]). Here, we illustrate the wide variety of FAPs with a brief discussion of the most popular applications. Successively, we discuss in the next section radio and television broadcasting, cellular telephone networks (both terrestrial and satellite based), and fixed location wireless telecommunication networks.
Till the large-scale introduction of cable television and satellite broadcasting in the beginning of the 1980s, the most convenient way to transmit radio and television signals was (and still is for radio) through the air. To cover an area for radio or television broadcasting, antennae scattered around the region are necessary. For radio, each of these antennae transmits in a radial way either an Amplitude Modulated (AM) or a Frequency Modulated (FM) signal. For AM signals frequencies in the range from 540 kHz to 1600 kHz (medium frequency spectrum) are used, whereas FM signals are transmitted on VHF frequencies in the range 87 MHz - 108 MHz.
Another part of the VHF spectrum and the UHF spectrum are explored to transmit television signals. As for radio, the television signal is not directed but transmitted in a radial way. The signal transmitted by an antenna may not interfere with other signals transmitted by other radio or television services in the same area. Moreover, in case two antennae of the same broadcasting service cover a part of the area simultaneously, the signals of these antennae are not allowed to interfere as well.
The development of (digital) cellular phone networks does not only attract the attention of the scientific community. In the last decade it has begun to influence the whole society. Cellular phone networks, however, have existed already for more than 50 years. As early as 1946, the first commercial mobile telephone service (MTS) was introduced by AT&T. Eighteen years later, AT&T introduced an improved version (IMTS). In this system 11 channels were available for all users within a geographic area. Since each frequency could be used only once (without interference), the IMTS system had a very limited capacity. In the New York region for example, the number of subscribers was limited to 545. In the late 1970s AT&T and Motorola Inc. developed the advanced mobile phone system (AMPS). AMPS had at its disposal 666 paired voice channels. These 666 channels made it possible to serve a large population. The system, publicly introduced in 1983, had 200,000 subscribers after the first year and 2,000,000 five years later. To increase the capacity even further, 166 additional channels were made available for the AMPS. Systems like the AMPS were also developed in Japan (1979) and Europe, starting in Scandinavia in 1981.
A disadvantage of the systems available during the 1980s in Europe was their mutual incompatibility. Therefore, in 1988 the Groupe Speciale Mobile (GSM) was founded by a group of government-owned telephone companies. They developed a new digital-based mobile communication standard, which has been in use since 1992. GSM networks use frequencies in the 900 Mhz and 1800 Mhz spectrum (UHF). The GSM system became an overwhelming success, not only in Europe, but currently all around the world. At the end of 1998 a total of 320 networks in 118 countries were serving approximately 135 million customers. For more recent figures, click here.
A third generation of mobile communication will be introduced in the near future. UMTS (Universal Mobile Telecommunications System) will replace GSM as the new world wide standard for cellular phone networks. In contrast to the current GSM system, UMTS will be compatible in both Europe and the United States of America. UMTS will use high speed connections (up to 2 megabit per second), enabling mobile use of internet and video communication.
All terrestrial cellular phone systems can be characterized by the following properties. They consist of a number of base stations that divide a geographic area to be served in smaller areas, called cells. Each base station operates on a certain frequency. A cellular phone within a cell is connected with the base station upon request via this frequency. As a mobile phone proceeds from one cell to another during a call, a mobile telephone switching office arranges that the call continues without noticeable interruption. If the demand for the wireless service within a cell exceeds the capacity of the base station, splitting the cell into smaller cells can increase the capacity. Depending on the geographical position, the power of the signal and the direction in which the signal is transmitted, transceivers may interfere when they use (almost) the same frequency.
The rapid development of cellular telephone networks in recent years has increased the need for good solution techniques for the frequency assignment problem for cellular networks. A main difference between radio / television broadcasting and cellular phone networks is the need for an individual connection for every customer. In radio and television networks thousands or even millions of customers receive the same signal transmitted by one single antenna. In a cellular phone network, a signal is transmitted only between one transmitter and one receiver. Technological developments such as Frequency Division Multiple Access (FDMA), Time Division Multiple Access (TDMA), and Code Division Multiple Access (CDMA) make it possible to use a frequency simultaneously for a limited number of different customers within the same cell. Nevertheless, the service area of a cellular network has to be covered with quite a large number of antennae to satisfy the demand. In a country like the Netherlands for example, a radio or television network can cover the area with less than a dozen transmitters. In contrast, the number of transmitters needed to cover the same area for a mobile phone service can be as large as a couple of thousands. Combined with about 40 available frequencies, we have to conclude that each frequency must be reused many times. Fortunately, the low transmitting power of battery-operated portable phones offers the opportunity to increase the reuse of frequencies within the same service area without interference.
Not only, the scale of the cellular radio networks, but also the investments related to it, strengthen the need for good frequency plans. Let us illustrate the importance of a good assignment by the investments related to GSM networks in the Netherlands. The three providers Telfort, Dutchtone, and Ben reputedly paid altogether 1.8 billion guilders for the frequencies in the 1800 Mhz spectrum that were sold at an auction in 1998. Besides this investment, the building of a cellular network costs at least 300 million guilders. However, all these efforts are worthless without a good frequency plan that can guarantee high-quality communication links to the customers.
In addition to the terrestrial systems, in recent years satellite-based telephone systems have been under construction. With such a system it is possible to make a connection with a cellular phone all around the world, especially in those regions currently not covered by a terrestrial system. In contrast with other satellite communication systems, satellite-based phone systems operate in the Low Earth Orbit (780 km high), and are therefore called LEO systems. The satellites work differently from those at a much higher orbit (36,000 km) in two major ways. First, the small distance between earth and satellite makes it possible to connect to the system with a handheld device. Second, signals can be moved overhead in between satellites without the use of base stations on the earth. In the near future, operators will supply services in which terrestrial and satellite communication are integrated.
Like in the terrestrial systems, the satellites operate on certain frequencies, that have to be selected in such a way that interference is avoided. Not only frequencies are needed to communicate with handheld devices, but also to establish communication between satellites and ground stations, and between satellites mutually.
One of the most recent applications of wireless communication is the establishment of fixed cellular telecommunication networks. In contrast to mobile cellular networks, in non-mobile or fixed systems both the transmitters and receivers are located at fixed points in the area. Fixed cellular networks provide a financially attractive alternative to the construction of conventional wired networks in developing countries, where no wired network structure is available yet. Moreover, the introduction of new services, such as data communication (internet, e-mail) and video-conferencing causes shortage of capacity in existing wired networks. Point-to-point wireless connections can be used as an alternative to the extension of the capacity of these wired networks. In both cases no cable connections have to be established. A disadvantage of point-to-point connections is that the transmitter and receiver have to see each other, which means that there should be no obstacles in between them. As a consequence, transmitters and receivers have to be built at high locations (e.g., at the roof of apartment and office buildings). Although the transmitters are directed to the receivers their signals can interfere. Especially if signals cross each other, the use of (almost) the same frequencies should be avoided.
Another application that has similarities with fixed cellular networks stems from the military. In military communication networks, wireless connections have to be established between pairs of transceivers. These connections, or radio links, can interfere with each other, if they use similar frequencies in one and the same area.
The purpose of a point-to-multipoint radio access system (PMP-system) is to supply wireless access to voice/data communication networks. Base stations form the access points to the network. Costumer terminals are linked to base stations by means of radio signals, where some specific part of the radio frequency spectrum has to be used to maintain the links. In contrast to cellular phone networks, each costumer is provided a fixed antenna and is assigned to a certain sector of a base station. A central problem is that a link connecting a costumer terminal and a base station may be subject to interference from another link, provided that the same frequency is used. To guarantee an interference-free communication, two frequency assignment problems have to be solved when operating a PMP-system, namely, the bandwidth allocation and the broadcast channel assignment. The bandwidth allocation is the problem of assigning a frequency interval within the available radio frequency spectrum to each costumer (link). The goal is to identify span-minimal frequency plans, taking into account the individual communication demand of each costumer and several technical and legal restrictions. The broadcast channel problem consists in assigning one further (unit demand) channel to each sector of a base station. This channel is required for signaling purposes between the base station and the customer terminals within its sectors. The goal is to provide a broadcast channel to each sector without causing interference among the sectors such that a minimal number of channels is used.
The frequency band [fmin,fmax] available to some provider of wireless
communication is usually partitioned into a set of channels, all with the same bandwidth
![]() of frequencies. For this reason the channels are usually numbered from 1 to a
given maximum N, where
of frequencies. For this reason the channels are usually numbered from 1 to a
given maximum N, where ![]() . The available channels are
denoted by the domain
. The available channels are
denoted by the domain ![]() . For a particular connection possibly not all
channels from D are available. For instance, if this connection is close to the
border of a country, division rules between the countries involved may lead to a
substantial decrease in channel availability. Therefore, the channels available for a
connection v form a subset
. For a particular connection possibly not all
channels from D are available. For instance, if this connection is close to the
border of a country, division rules between the countries involved may lead to a
substantial decrease in channel availability. Therefore, the channels available for a
connection v form a subset ![]() . On each channel available one can
communicate information from a transmitter to a receiver. For bidirectional traffic
one needs two such channels, one for each direction. In the models considered in the
literature the second channel is almost always ignored. The reasons for ignoring this
aspect of the FAP depend on the application. Instead of one band [fmin,fmax],
in most applications two bands [fmin1,fmax1] and [fmin2,fmax2] of
N channels are available: one with the channels
. On each channel available one can
communicate information from a transmitter to a receiver. For bidirectional traffic
one needs two such channels, one for each direction. In the models considered in the
literature the second channel is almost always ignored. The reasons for ignoring this
aspect of the FAP depend on the application. Instead of one band [fmin,fmax],
in most applications two bands [fmin1,fmax1] and [fmin2,fmax2] of
N channels are available: one with the channels ![]() , and one with the
channels
, and one with the
channels ![]() , where
, where ![]() . Thus, the backward connection uses a
channel which is shifted s channels up. The choice of s prevents any interference
of backward channels with forward channels. As a consequence, each assignment for the
forward channels can directly be transformed to an assignment for the backward
channels with similar performance.
. Thus, the backward connection uses a
channel which is shifted s channels up. The choice of s prevents any interference
of backward channels with forward channels. As a consequence, each assignment for the
forward channels can directly be transformed to an assignment for the backward
channels with similar performance.
Interference of signals is measured by the signal-to-noise ratio (or
signal-to-interference ratio) at the receiving end of a connection. There, the signal
transmitted should be clearly understandable. The noise comes from other signals which
have an interfering frequency on which they broadcast. There may be more than one
source that transmits on the same or a close frequency and thus contribute to the
total noise experienced at the receiver. In practice, a threshold value of 12 dB or 15
dB for the signal-to-noise ratio is found satisfactory. The computation of the level
of interference is a difficult job in itself, since it depends not only on signal
choice and strength, but also on the shape of the environment. If we ignore the
environment and consider some other signal transmitted at the same frequency channel,
then the interference of this signal at the receiver is computed with the following
formula: ![]() where P is the power of the transmitter and d the
distance to the disturbed receiver. Here,
where P is the power of the transmitter and d the
distance to the disturbed receiver. Here, ![]() is a fading factor with values
between 2 and 4. If this other signal is transmitted at a frequency at a distance of
is a fading factor with values
between 2 and 4. If this other signal is transmitted at a frequency at a distance of
![]() units of the original signal, then a filtering factor of
units of the original signal, then a filtering factor of ![]() is to be taken into account (see [Dunkin and Allen, 1997]). The fact that multiple signals may
disturb communication quality is ignored in most models, where only interference
between pairs of connections is measured. A notable exception
is [Fischetti et al., 1998], in which constraints are developed to determine the total
interference of neighboring connections. Another assumption is the quantification of
the levels of interference. We will assume given values of the interference as input
to our models and problems.
is to be taken into account (see [Dunkin and Allen, 1997]). The fact that multiple signals may
disturb communication quality is ignored in most models, where only interference
between pairs of connections is measured. A notable exception
is [Fischetti et al., 1998], in which constraints are developed to determine the total
interference of neighboring connections. Another assumption is the quantification of
the levels of interference. We will assume given values of the interference as input
to our models and problems.
The previously discussed two-way traffic poses another problem, even in the case where only interference between pairs of connections is taken into account. Interference need not be symmetric: if a transceiver (a single unit containing a transmitter and a receiver) pair (r1,r2) transmits on frequencies f and f+s, and another transceiver pair (s1,s2) transmits on frequencies g and g+s where f and g interfere, and f+s and g+s interfere, interference levels at r1 and r2 may be different due to the fact that these transceivers may have different distances to s1 and s2. As mentioned before, this aspect is ignored in most of the literature.
Depending on the application, one or multiple connections have to be established
between the same geographic end points. In general, this is modeled by assuming that
![]() frequencies have to be assigned to connection v. Interference
between frequencies assigned to the same connection can be avoided by the introduction
of an additional value for certain combinations of frequencies
frequencies have to be assigned to connection v. Interference
between frequencies assigned to the same connection can be avoided by the introduction
of an additional value for certain combinations of frequencies ![]() . In
practice the values cv vary during time, depending on the actual demand for
connections. By this property, the approaches suggested in the literature to deal with
the FAP can be divided into three categories: Fixed Channel Assignment (FCA), Dynamic
Channel Assignment (DCA), and Hybrid Channel Assignment (HCA) schemes (The
need for multiple connections, and the application of DCA and HCA schemes originates
from cellular phone networks).
. In
practice the values cv vary during time, depending on the actual demand for
connections. By this property, the approaches suggested in the literature to deal with
the FAP can be divided into three categories: Fixed Channel Assignment (FCA), Dynamic
Channel Assignment (DCA), and Hybrid Channel Assignment (HCA) schemes (The
need for multiple connections, and the application of DCA and HCA schemes originates
from cellular phone networks).
In an FCA the forecasted demand is transformed to the requirement that we have to assign to each connection a number of frequencies beforehand. In this scheme it is not allowed to change the assignment on-line to satisfy actual demand for wireless connections. This is in contrast with DCA schemes in which frequencies are assigned on-line to the connections in such a way that the actual demand is satisfied and the interference is minimized. An example of a procedure for DCA is presented by Janssen, Kilakos and Marcotte [Janssen et al., 1999]. They discuss a fixed preference assignment scheme. For every cell there exists a preference list of frequencies to serve the demand. In [Janssen et al., 1999] it is proved that the preference lists can be constructed in such a way, that they are optimal according to some performance measure.
Finally, in HCA schemes a combination of FCA and DCA is implemented to obtain a better overall performance of the network. In HCA schemes a number of frequencies is assigned to every connection beforehand, whereas another part of the spectrum can be used for on-line assignment of frequencies upon request. An example of an HCA scheme is given by Sandalidis, Stavroulakis and Rodriguez-Tellez [Sandalidis et al., 1999], who describe a neural network and a genetic algorithm approach to the borrowing channel assignment problem. In the borrowing channel assignment problem, a fixed number of frequencies are assigned to the connections. However, whenever the actual demand for frequencies exceeds the number of available frequencies, the connection can borrow an unused frequency assigned to an adjacent connection. The performance of networks that operate on DCA and HCA schemes is mostly studied via simulation of the particular procedure. It is proved by Johri [Johri, 1994] that DCA schemes perform better than FCA schemes under light traffic and under nonuniform traffic. However, under uniform and heavy load, FCA schemes outperform the DCA schemes. Besides this, FCA gives a bound on the performance of the DCA scheme. In fact, in case the DCA scheme allows for complete rearrangement of the assignment, a FCA problem has to be solved, every time the situation changes. For these last two reasons, we concentrate in the sequel on fixed channel assignment. For a survey on the topic of FCA, DCA and HCA schemes we refer to Katzela and Naghshineh [Katzela and Naghshineh, 1996].
The approaches to solve the FAP can be subdivided in two main streams. We want to assign frequencies to the vertices in such a way that either the total penalty incurred by a solution (minsum) or maximum penalty incurred by a solution (minmax) is minimized.
In case the incurred penalties exceed the given threshold in every assignment, two directions remain. On the one hand, the threshold value can be increased allowing for assignments with more interference. On the other hand, we can search for a partial assignment that does not exceed the given threshold penalty. The most common objective to distinguish between partial assignments is minimization of the blocking probability. In case instead of the requested cv only mv frequencies can be assigned to a connection, we can calculate the probability that in practice a request to establish a connection have to be rejected. This probability is called the blocking probability of the connection. Optimal partial assignments minimize the overall blocking probability of the network.
Summarized, we can distinguish four models to solve the FAP. In this chapter we discuss these four most common points of view:
MINIMUM ORDER FREQUENCY ASSIGNMENT (MO-FAP)
INSTANCE: Undirected graph G = (V,E), ![]() , for
all
, for
all ![]() , sets
, sets ![]() ,
, ![]() ,
, ![]() , demand
, demand ![]() , domain subsets
, domain subsets ![]() for all
for all ![]() ,
, ![]() , and positive integer K.
, and positive integer K.
QUESTION: Does there exist an assignment of subsets ![]() such that,
such that,
The MO-FAP is the first frequency assignment problem that is discussed in the literature. In most articles, Metzger [Metzger, 1970] has received the credits for bringing the MO-FAP to the attention of the Operations Research society (cf. Hale [Hale, 1980]). This problem is a direct generalization of the graph coloring problem.
MINIMUM SPAN FREQUENCY ASSIGNMENT (MS-FAP)
INSTANCE: Undirected graph G = (V,E), ![]() , for
all
, for
all ![]() , sets
, sets ![]() ,
, ![]() ,
, ![]() , demand
, demand ![]() , domain subsets
, domain subsets ![]() for all
for all ![]() ,
, ![]() , and positive integer K.
, and positive integer K.
QUESTION: Does there exist an assignment of subsets ![]() such that,
such that,
MINIMUM BLOCKING FREQUENCY ASSIGNMENT (MB-FAP)
INSTANCE: Undirected graph G = (V,E), ![]() , for
all
, for
all ![]() , sets
, sets ![]() ,
, ![]() ,
, ![]() , demand
, demand ![]() , domain subsets
, domain subsets ![]() for all
for all ![]() ,
, ![]() , non-increasing blocking function
, non-increasing blocking function ![]() for all
for all
![]() , and positive integer K.
, and positive integer K.
QUESTION: Does there exist an assignment of subsets ![]() such that,
such that,
The special case in which cv = 1, bv(0) = 1, bv(1) = 0, |Dv|=1, Dv
= Dw for all ![]() , and
, and ![]() for all
for all ![]() , is equivalent with
the maximum independent set problem. As a consequence, MB-FAP is
, is equivalent with
the maximum independent set problem. As a consequence, MB-FAP is ![]() -complete in
general.
-complete in
general.
MINIMUM INTERFERENCE FREQUENCY ASSIGNMENT
INSTANCE: Undirected graph G = (V,E), ![]() , for all
, for all ![]() , sets
, sets ![]() ,
, ![]() ,
, ![]() , demand
, demand ![]() , domain subsets
, domain subsets ![]() for all
for all ![]() ,
, ![]() , penalty values
, penalty values ![]() , for all
, for all ![]() ,
, ![]() ,
, ![]() , and positive integer K.
, and positive integer K.
QUESTION: Does there exist an assignment of subsets ![]() such that,
such that,
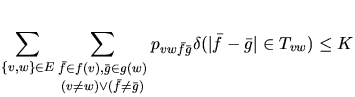 ?
?
In many cases the MI-FAP is used as a subroutine to find the minimum span of a FAP. In this special case we would like to find an interference-free assignment to the vertices, i.e., K=0. This problem is also known as the FEASIBILITY FREQUENCY ASSIGNMENT problem.
FEASIBILITY FREQUENCY ASSIGNMENT
INSTANCE: Undirected graph G = (V,E), ![]() , for all
, for all ![]() ,sets
,sets ![]() ,
, ![]() ,
, ![]() , demand
, demand ![]() ,and domain subsets
,and domain subsets ![]() for all
for all ![]() ,
, ![]() .
.
QUESTION: Does there exist an assignment of subsets ![]() such
that,
such
that,